在正方形ABCD中,AB=4.
(1)正方形ABCD的周长为 ;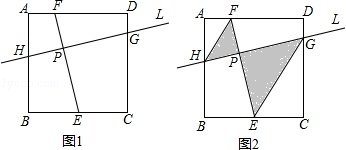
(2)如图1,点E、F分别在BC和AD上,点P是线段EF上的动点,过点P作EF的垂线L,若直线L与正方形CD、AB的交点分别在G、H.
①求证:EF=GH;
②已知,BE=2,AF=1,若线段PE的长度为a,求a的最小值;
③如图2,在②的条件下,已知AH=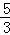 ,PE=2PF,求图中阴影部分的面积.
,PE=2PF,求图中阴影部分的面积.
相关知识点
推荐套卷
在正方形ABCD中,AB=4.
(1)正方形ABCD的周长为 ;
(2)如图1,点E、F分别在BC和AD上,点P是线段EF上的动点,过点P作EF的垂线L,若直线L与正方形CD、AB的交点分别在G、H.
①求证:EF=GH;
②已知,BE=2,AF=1,若线段PE的长度为a,求a的最小值;
③如图2,在②的条件下,已知AH=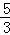 ,PE=2PF,求图中阴影部分的面积.
,PE=2PF,求图中阴影部分的面积.