如图,在直角坐标系中点A(2,0),点P在射线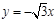 (x<0)上运动,设点P的横坐标为a,以AP为直径作⊙C,连接OP、PB,过点P作PQ⊥OP交⊙C于点Q.
(x<0)上运动,设点P的横坐标为a,以AP为直径作⊙C,连接OP、PB,过点P作PQ⊥OP交⊙C于点Q.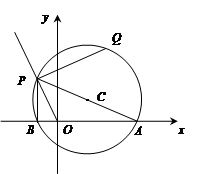
(1)证明:∠AOP=∠BPQ;
(2)当点P在运动的过程中,线段PQ的长度是否发生变化,若变化,请用含a的代数式表示PQ的长;若不变,求出PQ的长;
(3)当tan∠APO=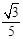 时,①求点Q坐标;②点D是圆上任意一点,求QD+
时,①求点Q坐标;②点D是圆上任意一点,求QD+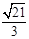 OD的最小值.
OD的最小值.
相关知识点
推荐套卷
如图,在直角坐标系中点A(2,0),点P在射线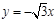 (x<0)上运动,设点P的横坐标为a,以AP为直径作⊙C,连接OP、PB,过点P作PQ⊥OP交⊙C于点Q.
(x<0)上运动,设点P的横坐标为a,以AP为直径作⊙C,连接OP、PB,过点P作PQ⊥OP交⊙C于点Q.
(1)证明:∠AOP=∠BPQ;
(2)当点P在运动的过程中,线段PQ的长度是否发生变化,若变化,请用含a的代数式表示PQ的长;若不变,求出PQ的长;
(3)当tan∠APO=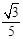 时,①求点Q坐标;②点D是圆上任意一点,求QD+
时,①求点Q坐标;②点D是圆上任意一点,求QD+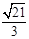 OD的最小值.
OD的最小值.