【试题背景】已知:l ∥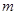 ∥
∥ ∥k,平行线l与
∥k,平行线l与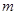 、
、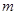 与
与 、
、 与k之间的距离分别为
与k之间的距离分别为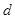 1、
1、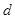 2、
2、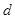 3,且
3,且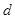 1 =
1 =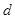 3 = 1,
3 = 1,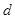 2 =" 2" .我们把四个顶点分别在l、
2 =" 2" .我们把四个顶点分别在l、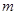 、
、 、k这四条平行线上的四边形称为“格线四边形”.
、k这四条平行线上的四边形称为“格线四边形”.
【探究1】(1)如图1,正方形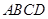 为“格线四边形”,
为“格线四边形”, 于点
于点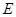 ,
,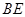 的反向延长线交直线k于点
的反向延长线交直线k于点 . 求正方形
. 求正方形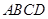 的边长.
的边长.
【探究2】(2)矩形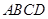 为“格线四边形”,其长 :宽 =" 2" :1 ,则矩形
为“格线四边形”,其长 :宽 =" 2" :1 ,则矩形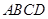 的宽为 .(直接写出结果即可)
的宽为 .(直接写出结果即可)
【探究3】(3)如图2,菱形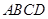 为“格线四边形”且∠
为“格线四边形”且∠ =60°,△
=60°,△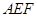 是等边三角形,
是等边三角形, 于点
于点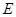 , ∠
, ∠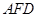 =90°,直线
=90°,直线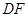 分别交直线l、k于点
分别交直线l、k于点 、
、 . 求证:
. 求证: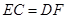 .
.
【拓 展】(4)如图3,l ∥k,等边三角形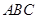 的顶点
的顶点 、
、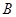 分别落在直线l、k上,
分别落在直线l、k上,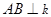 于点
于点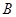 ,且
,且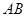 ="4" ,∠
="4" ,∠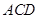 =90°,直线
=90°,直线 分别交直线l、k于点
分别交直线l、k于点 、
、 ,点
,点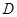 、
、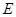 分别是线段
分别是线段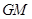 、
、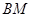 上的动点,且始终保持
上的动点,且始终保持 =
=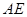 ,
, 于点
于点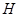 .
.
猜想: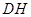 在什么范围内,
在什么范围内, ∥
∥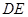 ?直接写出结论。
?直接写出结论。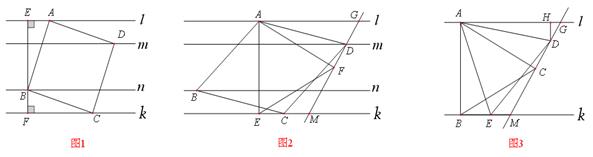
相关知识点
推荐套卷




 粤公网安备 44130202000953号
粤公网安备 44130202000953号