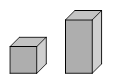
如图1是立方体和长方体模型,立方体棱长和长方体底面各边长都为1,长方体侧棱长为2,现用60张长为6宽为4的长方形卡纸,剪出这两种模型的表面展开图,有两种方法:
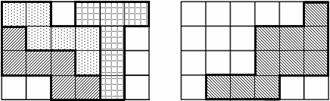
方法一:如图2,每张卡纸剪出3个立方体表面展开图;
方法二:如图3,每张卡纸剪出2个长方体表面展开图(图中只画出1个).
|
设用x张卡纸做立方体,其余卡纸做长方体,共做两种模型y个.
(1)在图3中画出第二个长方体表面展开图,用阴影表示;
(2)写出y关于x的函数解析式;
(3)设每只模型(包括立方体和长方体)平均获利为w(元),w满足函数
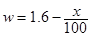 ,若想将模型作为教具卖出,且制作的长方体的个数不超过立方体的个数,则应该制作立方体和长方体各多少个,使获得的利润最大?最大利润是多少?
,若想将模型作为教具卖出,且制作的长方体的个数不超过立方体的个数,则应该制作立方体和长方体各多少个,使获得的利润最大?最大利润是多少?相关知识点
推荐套卷



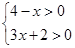 ,并把它的解集在数轴上表示出来.
,并把它的解集在数轴上表示出来. 。
。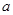 与
与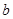 的大小,可先求出
的大小,可先求出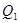 元,乙两次购买粮食的平均单价为
元,乙两次购买粮食的平均单价为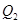 元,
元, 粤公网安备 44130202000953号
粤公网安备 44130202000953号