2014年12月28日“青烟威荣”城际铁路正式开通,从烟台到北京的高铁里程比普快里程缩短了81千米,运行时间减少了9小时,已知烟台到北京的普快列车里程月1026千米,高铁平均时速是普快平均时速的2.5倍.
(1)求高铁列车的平均时速;
(2)某日王老师要去距离烟台大约630千米的某市参加14:00召开的会议,如果他买到
当日8:40从烟台到该是的高铁票,而且从该市火车站到会议地点最多需要1.5小时.试问在高铁列车准点到达的情况下他能在开会之前赶到吗?
相关知识点
推荐套卷

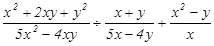 的值.
的值. ,
, ,
, ,将此三角板绕原点
,将此三角板绕原点 顺时针旋转
顺时针旋转 ,得到
,得到 .
. ,求该抛物线解析式;
,求该抛物线解析式; 是在第一象限内抛物线上一动点,求使四边形
是在第一象限内抛物线上一动点,求使四边形 的面积达到最大时点
的面积达到最大时点
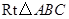 中,斜边
中,斜边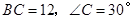 ,
, 为
为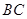 的中点,
的中点,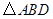 的外接圆
的外接圆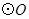 与
与 交于
交于 点,过
点,过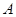 作
作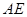 交
交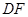 的延长线于
的延长线于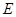 点.
点.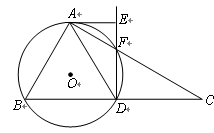
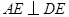 ;
;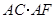 的值.
的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号