如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m.
(1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?
(2)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?
相关知识点
推荐套卷
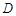 ,AE交BD于点C,且BC=DC.求证AB=ED.
,AE交BD于点C,且BC=DC.求证AB=ED.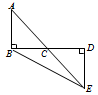
 、
、 、
、 、
、 四点在一直线上,AF=CD,AB∥DE,且AB=DE,求证:△ABC≌△DEF.
四点在一直线上,AF=CD,AB∥DE,且AB=DE,求证:△ABC≌△DEF.

 ,且l与x轴、y轴分别交于A、B两点,动点Q从B点开始在线段BA上以每秒2个单位的速度向点A移动,同时动点P从A点开始在线段AO上以每秒1个单位的速度向O点移动,设点Q、P移动时间为t秒。
,且l与x轴、y轴分别交于A、B两点,动点Q从B点开始在线段BA上以每秒2个单位的速度向点A移动,同时动点P从A点开始在线段AO上以每秒1个单位的速度向O点移动,设点Q、P移动时间为t秒。
 粤公网安备 44130202000953号
粤公网安备 44130202000953号