探究:如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE,
结论:(1)∠AEB的度数为 ;
(2)线段AD、BE之间的数量关系是 .
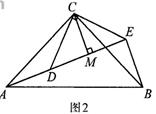
应用:如图2,△ACB和△DCE均为等腰三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM、AE、BE之间的数量关系,并说明理由.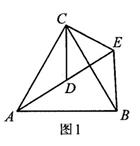
相关知识点
推荐套卷
探究:如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE,
结论:(1)∠AEB的度数为 ;
(2)线段AD、BE之间的数量关系是 .
应用:如图2,△ACB和△DCE均为等腰三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM、AE、BE之间的数量关系,并说明理由.
