作图题(不写作法,保留作图痕迹;共8分)
小河的同旁有甲、乙两个村庄,现计划在河岸AB上建一个水泵站,向两村供水,用以解决村民生活用水问题.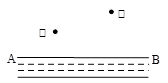
(1)如果要求水泵站到甲、乙两村庄的距离相等,水泵站M应建在河岸AB上的何处?
(2)如果要求建造水泵站使用建材最省,水泵站P又应建在河岸AB上的何处?
相关知识点
推荐套卷
作图题(不写作法,保留作图痕迹;共8分)
小河的同旁有甲、乙两个村庄,现计划在河岸AB上建一个水泵站,向两村供水,用以解决村民生活用水问题.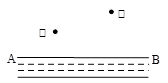

(1)如果要求水泵站到甲、乙两村庄的距离相等,水泵站M应建在河岸AB上的何处?
(2)如果要求建造水泵站使用建材最省,水泵站P又应建在河岸AB上的何处?