某商场计划拨款9万元从厂家购进50台电视机,已知该厂家生产三种不同型号的电视机,出厂价分别为:甲种每台1500元,乙种每台2100元,丙种每台2500元.
(1)若商场同时购进其中两种不同型号电视机共50台,用去9万元,请你研究一下商场的进货方案;
(2)若商场销售一台甲种电视机可获利150元,销售一台乙种电视机可获利200元,销售一台丙种电视机可获利250元.在同时购进两种不同型号电视机的方案中,为使销售利润最多,你选择哪一种进货方案?
相关知识点
推荐套卷

 道题.
道题.
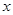 、
、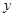 的方程组
的方程组 的解是正数,且
的解是正数,且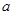 的范围。
的范围。 粤公网安备 44130202000953号
粤公网安备 44130202000953号