阅读下面的材料:
小明遇到一个问题:如图1,在□ABCD中,点E是边BC的中点,点F是线段AE上一点,BF的延长线交射线CD于点G.如果 ,求
,求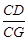 的值.
的值.
他的做法是:过点E作EH∥AB交BG于点H,那么可以得到△BAF∽△HEF.
请回答:
(1)AB和EH之间的数量关系是 ,CG和EH之间的数量关系是 ,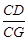 的值为 .
的值为 .
(2)参考小明思考问题的方法,解决问题:
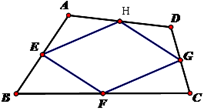
如图2,在四边形ABCD中,DC∥AB,点E是BC延长线上一点,AE和BD相交于点F.如果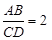 ,
,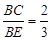 ,求
,求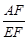 的值.
的值.
相关知识点
推荐套卷
 的图象与反比例函数
的图象与反比例函数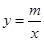 的图象交于A
的图象交于A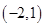 ,B
,B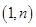 两点,
两点,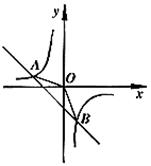
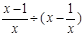 再从0、1、2中选取一个作为x的值代入求值.
再从0、1、2中选取一个作为x的值代入求值.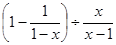
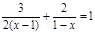
 粤公网安备 44130202000953号
粤公网安备 44130202000953号