(本小题满分13分)已知函数 ,其中
,其中 .
.
(1)当 时,求函数
时,求函数 的图象在点
的图象在点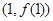 处的切线方程;
处的切线方程;
(2)当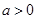 时,证明:存在实数
时,证明:存在实数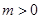 ,使得对于任意的实数
,使得对于任意的实数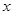 ,都有
,都有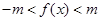 成立;
成立;
(3)当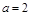 时,是否存在实数
时,是否存在实数 ,使得关于
,使得关于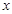 的方程
的方程 仅有负实数解?当
仅有负实数解?当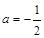 时的情形又如何?(只需写出结论).
时的情形又如何?(只需写出结论).
推荐套卷
(本小题满分13分)已知函数 ,其中
,其中 .
.
(1)当 时,求函数
时,求函数 的图象在点
的图象在点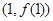 处的切线方程;
处的切线方程;
(2)当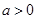 时,证明:存在实数
时,证明:存在实数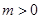 ,使得对于任意的实数
,使得对于任意的实数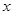 ,都有
,都有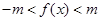 成立;
成立;
(3)当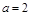 时,是否存在实数
时,是否存在实数 ,使得关于
,使得关于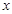 的方程
的方程 仅有负实数解?当
仅有负实数解?当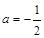 时的情形又如何?(只需写出结论).
时的情形又如何?(只需写出结论).