【问题探究】
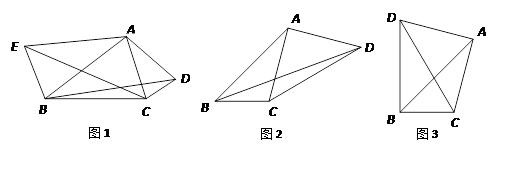
（1）如图1，锐角△ABC中，分别以AB、AC为边向外作等腰△ABE和等腰△ACD，使AE=AB，AD=AC，∠BAE=∠CAD，连接BD，CE，试猜想BD与CE的大小关系，并说明理由．
【深入探究】
（2）如图2，四边形ABCD中，AB=7cm，BC=3cm，∠ABC=∠ACD=∠ADC=45º，求BD的长．
（3）如图3，在（2）的条件下，当△ACD在线段AC的左侧时，求BD的长．
相关试题
，求使得
成立的
的集合
；
求实数m的值.
方程
与y轴交于A、B两点，圆心为P，若
.推荐套卷
【问题探究】
（1）如图1，锐角△ABC中，分别以AB、AC为边向外作等腰△ABE和等腰△ACD，使AE=AB，AD=AC，∠BAE=∠CAD，连接BD，CE，试猜想BD与CE的大小关系，并说明理由．
【深入探究】
（2）如图2，四边形ABCD中，AB=7cm，BC=3cm，∠ABC=∠ACD=∠ADC=45º，求BD的长．
（3）如图3，在（2）的条件下，当△ACD在线段AC的左侧时，求BD的长．
粤公网安备 44130202000953号