已知点P是∠MON的平分线上的一动点,射线PA交射线OM于点A,将射线PA绕点P逆时针旋转交射线ON于点B,且使∠APB+∠MON=1800.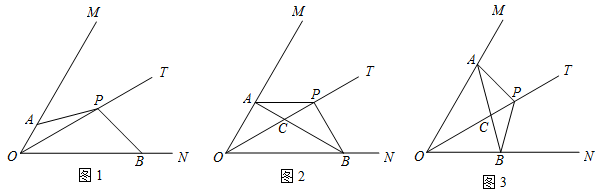
(1)利用图1,求证:PA=PB;
(2)如图2,若点 是
是 与
与 的交点,当
的交点,当 时,求PC与PB的比值;
时,求PC与PB的比值;
(3)若∠MON=60°,OB=2,射线AP交ON于点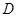 ,且满足且
,且满足且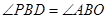 ,请借助图3补全图形,并求
,请借助图3补全图形,并求 的长.
的长.
推荐套卷
已知点P是∠MON的平分线上的一动点,射线PA交射线OM于点A,将射线PA绕点P逆时针旋转交射线ON于点B,且使∠APB+∠MON=1800.
(1)利用图1,求证:PA=PB;
(2)如图2,若点 是
是 与
与 的交点,当
的交点,当 时,求PC与PB的比值;
时,求PC与PB的比值;
(3)若∠MON=60°,OB=2,射线AP交ON于点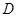 ,且满足且
,且满足且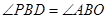 ,请借助图3补全图形,并求
,请借助图3补全图形,并求 的长.
的长.