水龙头关闭不严会造成滴水,容器内盛水时w(L)与滴水时间t(h)的关系用可以显示水量的容器做如图1的试验,并根据试验数据绘制出如图2的函数图象,结合图象解答下列问题.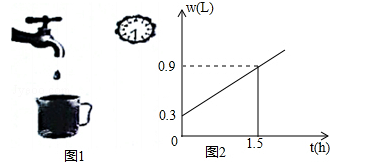
(1)容器内原有水多少升?
(2)求w与t之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升?
相关知识点
推荐套卷
水龙头关闭不严会造成滴水,容器内盛水时w(L)与滴水时间t(h)的关系用可以显示水量的容器做如图1的试验,并根据试验数据绘制出如图2的函数图象,结合图象解答下列问题.
(1)容器内原有水多少升?
(2)求w与t之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升?