【2015高考上海,理22】已知数列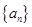 与
与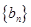 满足
满足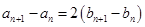 ,
,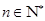 .
.
(1)若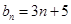 ,且
,且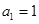 ,求数列
,求数列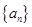 的通项公式;
的通项公式;
(2)设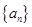 的第
的第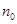 项是最大项,即
项是最大项,即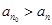 (
(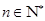 ),求证:数列
),求证:数列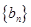 的第
的第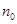 项是最大项;
项是最大项;
(3)设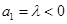 ,
,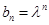 (
(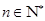 ),求
),求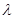 的取值范围,使得
的取值范围,使得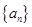 有最大值
有最大值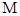 与最小值
与最小值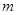 ,且
,且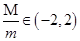 .
.
推荐套卷
【2015高考上海,理22】已知数列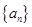 与
与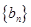 满足
满足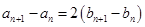 ,
,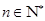 .
.
(1)若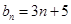 ,且
,且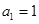 ,求数列
,求数列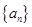 的通项公式;
的通项公式;
(2)设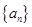 的第
的第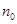 项是最大项,即
项是最大项,即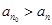 (
(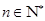 ),求证:数列
),求证:数列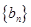 的第
的第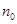 项是最大项;
项是最大项;
(3)设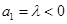 ,
,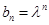 (
(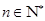 ),求
),求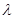 的取值范围,使得
的取值范围,使得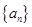 有最大值
有最大值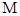 与最小值
与最小值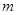 ,且
,且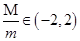 .
.