（（本小题满分12分）
一项"过关游戏"规则规定: 在第n 关要抛掷骰子n次, 若这n次抛掷所出现的点数之和大于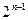
＋1 (n∈N*), 则算过关.
(1)求在这项游戏中第三关过关的概率是多少?
(2) 若规定n≤3, 求某人的过关数ξ的期望.
处的切线与直线
平行；
的单调区间；
，求函数
单调区间；
在区间（1，2）单调递减。
时，求a的取值范围；
的取值范围。
的图像按向量a=（2，—1）平移后，再作关于直线y=x的对称图像
推荐套卷
（（本小题满分12分）
一项"过关游戏"规则规定: 在第n 关要抛掷骰子n次, 若这n次抛掷所出现的点数之和大于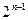＋1 (n∈N*), 则算过关.
(1)求在这项游戏中第三关过关的概率是多少?
(2) 若规定n≤3, 求某人的过关数ξ的期望.
粤公网安备 44130202000953号