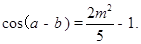【2015高考福建，理19】已知函数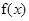
的图像是由函数
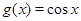的图像经如下变换得到：先将
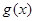图像上所有点的纵坐标伸长到原来的2倍（横坐标不变），再将所得到的图像向右平移
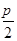个单位长度．
（Ⅰ）求函数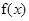的解析式，并求其图像的对称轴方程；
（Ⅱ）已知关于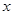
的方程
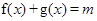在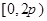
内有两个不同的解
．
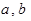（1）求实数m的取值范围；
（2）证明：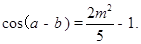
相关试题
圆铁皮剪出一个圆心角为
的扇形，制成一个圆锥形容器，扇形的圆心角
，
，
，求实数
的取值范围。
(x≠-a,a≠
).
的图象关于y=x对称，求a的值.。
，其中
为自然对数的底数．
的最小值；
，且
，证明：
．
；当年旅游业收八为400万元，预计今后的旅游业收入每年会比上一年增加
．
年的总投入为
万元，旅游业总收入为
万元，写出
）推荐套卷
【2015高考福建，理19】已知函数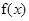的图像是由函数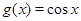的图像经如下变换得到：先将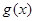图像上所有点的纵坐标伸长到原来的2倍（横坐标不变），再将所得到的图像向右平移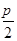个单位长度．
（Ⅰ）求函数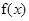的解析式，并求其图像的对称轴方程；
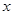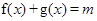（Ⅱ）已知关于的方程在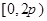内有两个不同的解．
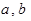（1）求实数m的取值范围；
（2）证明：
粤公网安备 44130202000953号