【2015高考湖南,文16】(本小题满分12分)某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖,抽奖方法是:从装有2个红球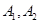 和1个白球
和1个白球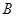 的甲箱与装有2个红球
的甲箱与装有2个红球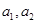 和2个白球
和2个白球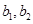 的乙箱中,各随机摸出1个球,若摸出的2个球都是红球则中奖,否则不中奖。
的乙箱中,各随机摸出1个球,若摸出的2个球都是红球则中奖,否则不中奖。
(Ⅰ)用球的标号列出所有可能的摸出结果;
(Ⅱ)有人认为:两个箱子中的红球比白球多,所以中奖的概率大于不中奖的概率,你认为正确吗?请说明理由。
推荐套卷
【2015高考湖南,文16】(本小题满分12分)某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖,抽奖方法是:从装有2个红球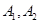 和1个白球
和1个白球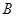 的甲箱与装有2个红球
的甲箱与装有2个红球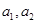 和2个白球
和2个白球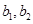 的乙箱中,各随机摸出1个球,若摸出的2个球都是红球则中奖,否则不中奖。
的乙箱中,各随机摸出1个球,若摸出的2个球都是红球则中奖,否则不中奖。
(Ⅰ)用球的标号列出所有可能的摸出结果;
(Ⅱ)有人认为:两个箱子中的红球比白球多,所以中奖的概率大于不中奖的概率,你认为正确吗?请说明理由。