已知:抛物线y=ax2+bx+c(a≠0)的对称轴为x=-1,与x轴交于A,B两点,与y轴交于点C,其中A(-3,0),C(0,-2).
(1)求这条抛物线的函数表达式;
(2)已知在对称轴上存在一点P,使得△PBC的周长最小.请求出点P的坐标;
(3)若点D是线段OC上的一个动点(不与点O、点C重合).过点D作DE∥PC交x轴于点E.连接PD、PE.设CD的长为m,△PDE的面积为S.求S与m之间的函数关系式.试说明S是否存在最大值?若存在,请求出最大值;若不存在,请说明理由.
相关知识点
推荐套卷


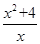 -4)÷
-4)÷  ,当
,当 满足
满足 且为正整数时,求代数式的值.
且为正整数时,求代数式的值. tan30°;(2)解方程:
tan30°;(2)解方程:
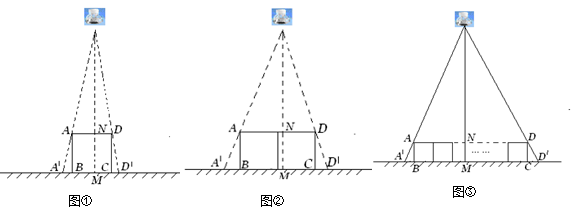 (2)不改变①中灯泡的高度,将两个边长为30cm的正方形框架按图②摆放,请计算此时横向影子A′B,D′C的长度和为多少?
(2)不改变①中灯泡的高度,将两个边长为30cm的正方形框架按图②摆放,请计算此时横向影子A′B,D′C的长度和为多少?


 粤公网安备 44130202000953号
粤公网安备 44130202000953号