某服装厂生产一种西装和领带，西装每套定价200元，领带每条定价40元。厂方在开展促销活动期间，向客户提供两种优惠方案：①买一套西装送一条领带；②西装和领带都按定价的90%付款．现某客户要到该服装厂购买西装20套，领带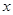
条（
）．
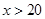（1）若该客户按方案①购买，需付款 元（用含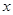的代数式表示）;
若该客户按方案②购买，需付款 元（用含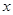的代数式表示）．
（2）请你通过计算帮该顾客设计较为合算购买方案？
相关试题
某服装厂生产一种西装和领带，西装每套定价200元，领带每条定价40元。厂方在开展促销活动期间，向客户提供两种优惠方案：①买一套西装送一条领带；②西装和领带都按定价的90%付款．现某客户要到该服装厂购买西装20套，领带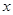条（）．
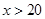（1）若该客户按方案①购买，需付款 元（用含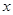的代数式表示）;
若该客户按方案②购买，需付款 元（用含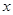的代数式表示）．
（2）请你通过计算帮该顾客设计较为合算购买方案？
的两个实数根，求该三角形的面积？
，求a、b的值
与直线
交于点O(0，0)，A(
，12)，点B是抛物线上O，A之间的一个动点，过点B分别作
轴、
轴的平行线与直线OA交于点C，E.
，
)，求出
粤公网安备 44130202000953号