（本题12分）如图，在平面直角坐标系中，矩形OABC的边OA在y轴的正半轴上，OC在x轴的正半轴上，∠AOC的平分线交AB于点D，E为BC的中点，已知A（0，4）、C（5，0），二次函数
的图象经过A、C两点．
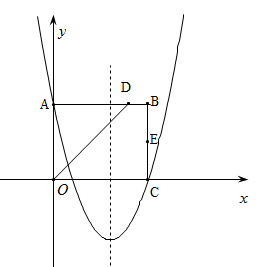
（1）求该二次函数的表达式；
（2）F、G分别为x轴、y轴上的动点，守卫顺次连结D、E、F、G构成四边形DEFG，求四边形DEFG周长的最小值；
（3）抛物线上是否存在点P，使△ODP的面积为12？若存在，求出点P的坐标；若不存在，请说明理由．
相关试题
如图①，四边形ABCD是正方形,G是BC上任意一点，DE⊥AG于点E，BF⊥AG于点F.
⑴求证：DE－BF=EF．
⑵当点G为BC边中点时,试探究线段EF与GF之间的数量关系，并说明理由．
⑶若点G为CB延长线上一点，其余条件不变．请你在图②中画出图形，写出此时DE、BF、EF之间的数量关系，并说明理由．
，
如图所示，点A坐标为（0，3），OA半径为1，点B在x轴上．
⑴若点B坐标为（4，0），⊙B半径为3，试判断⊙A与⊙B位置关系；
⑵若⊙B过M（-2，0）且与⊙A相切，求B点坐标．
，请你计算湖人队五场比赛成绩的平均得分
；相关知识点
推荐套卷
粤公网安备 44130202000953号