如图，有两条公路OM、ON相交成30°角，沿公路OM方向离O点80米处有一所学校A．当重型运输卡车P沿道路ON方向行驶时，在以P为圆心50米长为半径的圆形区域内都会受到卡车噪声的影响，且卡车P与学校A的距离越近噪声影响越大．若一直重型运输卡车P沿道路ON方向行驶的速度为18千米/时．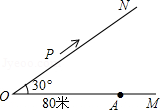
（1）求对学校A的噪声影响最大时卡车P与学校A的距离；
（2）求卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间．
相关试题
老师正叙述这样一道题：请同学们画出一个△ABC，然后画出AB，AC的中垂线，且交于点P．请同学们想一下点P到三角形三个顶点A，B，C的距离如何？小明马上就说：“相等．”他是随便说的吗？你同意他的说法吗？请说明你的理由．
相关知识点
推荐套卷
粤公网安备 44130202000953号