(本小题满分12分)某班50名学生在一次数学测试中,成绩全部介于50与100之间,将测试结果按如下方式分成五组:第一组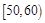 ,第二组
,第二组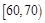 ,…,第五组
,…,第五组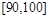 .下图是按上述分组方法得到的频率分布直方图.
.下图是按上述分组方法得到的频率分布直方图.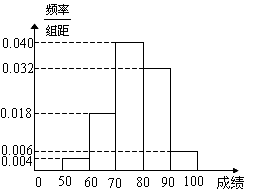
(Ⅰ)若成绩大于或等于60且小于80,认为合格,求该班在这次数学测试中成绩合格的人数;
(Ⅱ)从测试成绩在 内的所有学生中随机抽取两名同学,设其测试成绩分别为m、n,求事件“
内的所有学生中随机抽取两名同学,设其测试成绩分别为m、n,求事件“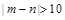 ”概率.
”概率.
推荐套卷
(本小题满分12分)某班50名学生在一次数学测试中,成绩全部介于50与100之间,将测试结果按如下方式分成五组:第一组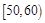 ,第二组
,第二组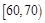 ,…,第五组
,…,第五组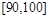 .下图是按上述分组方法得到的频率分布直方图.
.下图是按上述分组方法得到的频率分布直方图.
(Ⅰ)若成绩大于或等于60且小于80,认为合格,求该班在这次数学测试中成绩合格的人数;
(Ⅱ)从测试成绩在 内的所有学生中随机抽取两名同学,设其测试成绩分别为m、n,求事件“
内的所有学生中随机抽取两名同学,设其测试成绩分别为m、n,求事件“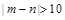 ”概率.
”概率.