某景点的门票价格如表:
| 购票人数/人 |
1~50 |
51~100 |
100以上 |
| 每人门票价/元 |
12 |
10 |
8 |
某校七年级(1)、(2)两班计划去游览该景点,其中(1)班人数少于50人,(2)班人数多于50人且少于100人,如果两班都以班为单位单独购票,则一共支付1118元;如果两班联合起来作为一个团体购票,则只需花费816元.
(1)两个班各有多少名学生?
(2)团体购票与单独购票相比较,两个班各节约了多少钱?
相关知识点
推荐套卷
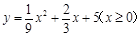 该镇那一年的国民生产总值可在1995年的基础上翻两番(即达到1995年的年国民生产总值的4倍)?
该镇那一年的国民生产总值可在1995年的基础上翻两番(即达到1995年的年国民生产总值的4倍)?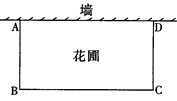
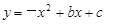 的部分图象如
的部分图象如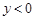 时,x的取值范围.
时,x的取值范围.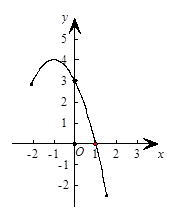
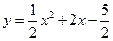 .
.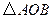 置于平面直角坐标系中,
置于平面直角坐标系中, 其中点
其中点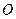 为坐标原点,点
为坐标原点,点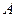 的坐标为
的坐标为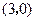 ,
,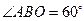 .
.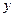 轴交于点
轴交于点 ,求
,求 粤公网安备 44130202000953号
粤公网安备 44130202000953号