如图，在平面直角坐标中，过点A（4，0）的抛物线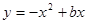
与直线
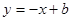交于另一点B．过抛物线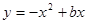的顶点E作EF⊥x轴于F点，点M（
，
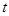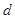）为抛物线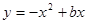在x轴上方的动点．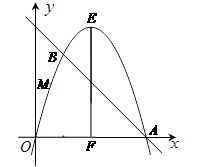
（1）填空：b＝ ；
（2）连结ME．当∠MEF＝30°时，请求出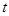的值；
（3）当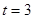
时，过点M作MC⊥x轴于C点，交AB于点N，连接ON．点Q为线段BN上一动点，过点Q作QR∥MN交ON于点R，连接MQ、BR．当∠MQR－∠BRN＝45°时，求点R的坐标．
相关知识点
推荐套卷
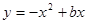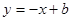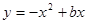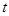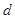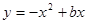如图，在平面直角坐标中，过点A（4，0）的抛物线与直线 交于另一点B．过抛物线的顶点E作EF⊥x轴于F点，点M（，）为抛物线在x轴上方的动点．
（1）填空：b＝ ；
（2）连结ME．当∠MEF＝30°时，请求出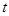的值；
（3）当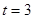时，过点M作MC⊥x轴于C点，交AB于点N，连接ON．点Q为线段BN上一动点，过点Q作QR∥MN交ON于点R，连接MQ、BR．当∠MQR－∠BRN＝45°时，求点R的坐标．
粤公网安备 44130202000953号