【问题】
如图①，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连接EF．求证：EF=BE+DF．
【思考】
将△ABE绕点A逆时针旋转90°至△ADE′的位置，易知点F、D、E′在一条直线上，由SAS可以证得△AE′F≌△AEF．由此得到：EF=E′F=DE′+DF=BE+DF．
【探究】
（1）如图②，在四边形ABCD中，点E、F分别在BC、CD上，AB=AD，∠B+∠D=180°，∠EAF=
∠BAD，BE=1，EF=2．2，求DF的长．
（2）将图②中的∠EAF绕点A旋转到如图③的位置，除去（1）中的条件BE=1，EF=2．2，其它条件不变时，探索线段EF、BE、DF之间的数量关系，并说明理由．
(每小题7分，共14分)
(1)计算：(2一
)2+(π一3.14) 0一(2+)-1；
(2)给出三个整式a2，b2和2ab，从中任意选择两个整式进行加法或减法运算，使所得的多项式能够因式分解．请写出你所选的式子及因式分解的过程．
(满分l3分)如图，对称轴为直线x=一
的抛物线经过点A(-6，0)和点B(0，4)．
(1)求抛物线的解析式和顶点坐标；
(2)设点E(x，y)是抛物线上的一个动点，且位于第三象限，四边形OEAF是以OA为对角线的平行四边形，求□OEAF的面积S与x的函数关系式，并写出自变量x的取值范围；
①当□OEAF的面积为24时，请判断□OEAF是否为菱形?
②是否存在点E，使□OEAF为正方形?若存在，求出点E的坐标；若不存在，请说明理由．
(满分l3分)如图，在△ABC中，∠A=90°，AB=4，AC=3，点M是AB上的动点(不与A，B重合)，过点M作MN∥BC交AC于点N．以MN为直径作⊙O，并在⊙O内作内接矩形AMPN，令AM=x．
(1)用含x的代数式表示△MNP的面积S；
(2)当x为何值时，⊙O与直线BC相切?
(满分l2分)学完“等边三角形”这一节后，老师布置了一道思考题：
如图，点M，N分别在正三角形ABC的BC，CA边上，且BM=CN，AM，BN交于点Q．
求证：∠BQM=60°．
(1)请你完成这道思考题；
(2)做完(1)后，同学们在老师的启发下进行了反思，提出了许多问题，如：
①若将题中“BM=CN”与“∠BQM=60°”的位置交换，得到的是否仍是真命题?
②若将题中的点M，N分别移动到BC，CA的延长线上，是否仍能得到∠BQM=60°?
③若将题中的条件“点M，N分别在正三角形ABC的BC，CA边上”改为“点M，N分别在正方形ABCD的BC，CD边上”，是否仍能得到∠BQM=60°?
请你作出判断，在下列横线上填写“是”或“否”：①______；②______；③______．并对②，③的判断，选择一个给出证明．
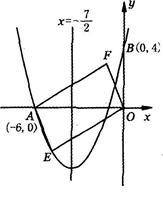
粤公网安备 44130202000953号