(1)过点P(-1,-2)的直线 分别交x轴和y轴的负半轴于A、B两点,当|PA|·|PB|最小时,求
分别交x轴和y轴的负半轴于A、B两点,当|PA|·|PB|最小时,求 的方程.
的方程.
(2)已知定点 与定直线
与定直线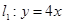 ,过
,过  点的直线
点的直线 与
与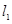 交于第一象限
交于第一象限 点,与x轴正半轴交于点
点,与x轴正半轴交于点 ,求使
,求使 面积最小的直线
面积最小的直线 方程。
方程。
推荐套卷
(1)过点P(-1,-2)的直线 分别交x轴和y轴的负半轴于A、B两点,当|PA|·|PB|最小时,求
分别交x轴和y轴的负半轴于A、B两点,当|PA|·|PB|最小时,求 的方程.
的方程.
(2)已知定点 与定直线
与定直线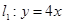 ,过
,过  点的直线
点的直线 与
与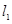 交于第一象限
交于第一象限 点,与x轴正半轴交于点
点,与x轴正半轴交于点 ,求使
,求使 面积最小的直线
面积最小的直线 方程。
方程。