在平面直角坐标系中,抛物线y=x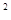 +5x+4的顶点为M,与x轴交于A、B两点与y轴交于C点。
+5x+4的顶点为M,与x轴交于A、B两点与y轴交于C点。
(1)求点A、B、C的坐标;
(2)求抛物线y=x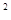 +5x+4关于坐标原点O对称的抛物线的函数表达式;
+5x+4关于坐标原点O对称的抛物线的函数表达式;
(3)设(2)中所求抛物线的顶点为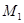 ,与x轴交于
,与x轴交于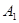 、
、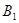 两点,与y轴交于
两点,与y轴交于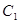 点,在以A、B、C、M、
点,在以A、B、C、M、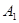 、
、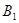 、
、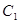 、、这八个点中的四个点为顶点的平行四边形中,求其中一个不是菱形的平行四边形的面积。
、、这八个点中的四个点为顶点的平行四边形中,求其中一个不是菱形的平行四边形的面积。
相关知识点
推荐套卷
在平面直角坐标系中,抛物线y=x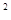 +5x+4的顶点为M,与x轴交于A、B两点与y轴交于C点。
+5x+4的顶点为M,与x轴交于A、B两点与y轴交于C点。
(1)求点A、B、C的坐标;
(2)求抛物线y=x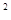 +5x+4关于坐标原点O对称的抛物线的函数表达式;
+5x+4关于坐标原点O对称的抛物线的函数表达式;
(3)设(2)中所求抛物线的顶点为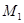 ,与x轴交于
,与x轴交于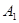 、
、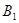 两点,与y轴交于
两点,与y轴交于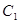 点,在以A、B、C、M、
点,在以A、B、C、M、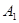 、
、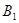 、
、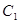 、、这八个点中的四个点为顶点的平行四边形中,求其中一个不是菱形的平行四边形的面积。
、、这八个点中的四个点为顶点的平行四边形中,求其中一个不是菱形的平行四边形的面积。