如图，在平面直角坐标系
中，已知抛物线
经过
，
两点，顶点为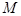
．
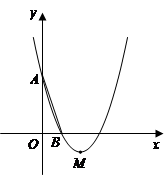
（1）求
、
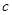的值；
（2）将
绕点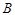
顺时针旋转90°后，点A落到点C的位置，该抛物线沿
轴上下平移后经过点
，求平移后所得抛物线的表达式；
（3）设（2）中平移后所得的抛物线与轴的交点为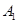
，顶点为
，若点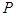
在平移后的抛物线上，且满足△
的面积是△
面积的3倍，求点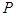的坐标．
相关试题
，连结
，
相交于点
，以点
为圆心，
cm长为半径画圆，试判断点
，
，
，
中，
，求证
，
，
，
四个顶点共圆．
的对角线
和
相交于
点，
，
，
，
分别是
，
，
，
的中点，求证：
相关知识点
推荐套卷
如图，在平面直角坐标系中，已知抛物线经过，两点，顶点为．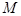
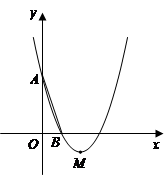
（1）求、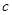的值；
（2）将绕点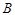顺时针旋转90°后，点A落到点C的位置，该抛物线沿轴上下平移后经过点，求平移后所得抛物线的表达式；
（3）设（2）中平移后所得的抛物线与轴的交点为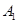，顶点为，若点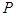在平移后的抛物线上，且满足△的面积是△面积的3倍，求点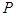的坐标．
粤公网安备 44130202000953号