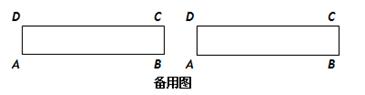
如图，ABCD是一张矩形纸片，AD=BC=1，AB=CD=5，在矩形ABCD的边AB上取一点M，在CD上取一点N，将纸片沿MN折叠，使MB与DN交于点K，得到△MNK。
（1）若∠1=70°，求∠MKN的度数；
（2）当折痕MN与对角线AC重合时，试求△MNK的面积．
（3）△MNK的面积能否小于0．5？若能，求出此时∠1的度数；若不能，试说明理由；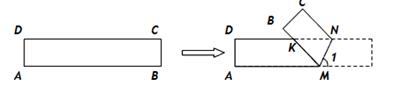
相关试题
与
－2成反比例，且当
时，求
（2）
相关知识点
推荐套卷
如图，ABCD是一张矩形纸片，AD=BC=1，AB=CD=5，在矩形ABCD的边AB上取一点M，在CD上取一点N，将纸片沿MN折叠，使MB与DN交于点K，得到△MNK。
（1）若∠1=70°，求∠MKN的度数；
（2）当折痕MN与对角线AC重合时，试求△MNK的面积．
（3）△MNK的面积能否小于0．5？若能，求出此时∠1的度数；若不能，试说明理由；
粤公网安备 44130202000953号