小颖为学校联欢会设计了一个“配紫色”的游戏;下面是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,游戏者同时转动两个转盘,如果转盘 转出了红色,转盘
转出了红色,转盘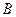 转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色.
转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色.

利用树状图或列表的方法表示出游戏所有可能出现的结果;
游戏者获胜的概率是多少?
相关知识点
推荐套卷
小颖为学校联欢会设计了一个“配紫色”的游戏;下面是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,游戏者同时转动两个转盘,如果转盘 转出了红色,转盘
转出了红色,转盘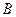 转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色.
转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色.

利用树状图或列表的方法表示出游戏所有可能出现的结果;
游戏者获胜的概率是多少?