(文)在平面直角坐标系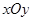 中,设锐角
中,设锐角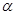 的始边与
的始边与 轴的非负半轴重合,终边与单位 圆交于点
轴的非负半轴重合,终边与单位 圆交于点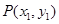 ,将射线
,将射线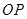 绕坐标原点
绕坐标原点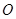 按逆时针方向旋转
按逆时针方向旋转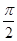 后与单位圆交于点
后与单位圆交于点 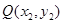 .记
.记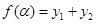 .(1)求函数
.(1)求函数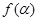 的值域;(2)设
的值域;(2)设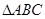 的角
的角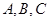 所对的边分别为
所对的边分别为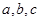 ,若
,若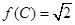 ,且
,且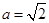 ,
,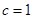 ,求
,求 .
.
相关知识点
推荐套卷
(文)在平面直角坐标系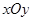 中,设锐角
中,设锐角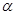 的始边与
的始边与 轴的非负半轴重合,终边与单位 圆交于点
轴的非负半轴重合,终边与单位 圆交于点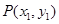 ,将射线
,将射线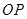 绕坐标原点
绕坐标原点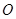 按逆时针方向旋转
按逆时针方向旋转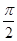 后与单位圆交于点
后与单位圆交于点 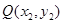 .记
.记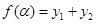 .(1)求函数
.(1)求函数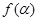 的值域;(2)设
的值域;(2)设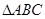 的角
的角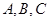 所对的边分别为
所对的边分别为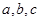 ,若
,若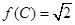 ,且
,且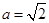 ,
,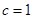 ,求
,求 .
.