(本小题满分9分)如图,已知直线l1∥l2,线段AB在直线l1上,BC垂直于l1交l2于点C,且AB=BC,P是线段BC上异于两端点的一点,过点P的直线分别交l2、 l1于点D、E(点A、E位于点B的两侧),满足BP=BE,连结AP、CE.
(1)求证:△ABP≌△CBE;
(2)连结AD、BD,BD与AP相交于点F,如图,
①当 时,求证:AP⊥BD;
时,求证:AP⊥BD;
② (n>1)时,设△PAD的面积为S1,△PCE的面积为S2,求
(n>1)时,设△PAD的面积为S1,△PCE的面积为S2,求 的值.
的值.
相关知识点
推荐套卷
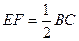 ;将AC沿BC方向平移到DH,得图(2),沿CB方向平移到DH得图(3),图(2)中AD与BH存在关系:EF∥AD,
;将AC沿BC方向平移到DH,得图(2),沿CB方向平移到DH得图(3),图(2)中AD与BH存在关系:EF∥AD, 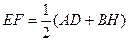 ;,那么在图(3)中是否有类似于图(1)(2)中的结论,请把猜想的结论填在方框内,并就图(3)的结论加以证明。
;,那么在图(3)中是否有类似于图(1)(2)中的结论,请把猜想的结论填在方框内,并就图(3)的结论加以证明。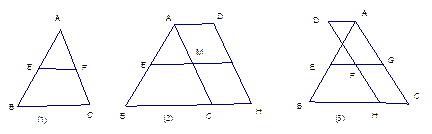

 粤公网安备 44130202000953号
粤公网安备 44130202000953号