（本小题满分12分）下图为某校语言类专业N名毕业生的综合测评成绩（百分制）分布直方图，已知80-90分数段的学员数为21人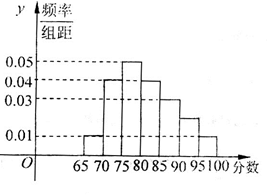
（1）求该专业毕业总人数N和90-95分数段内的人数
；
（2）现欲将90-95分数段内的名人分配到几所学校，从中安排2人到甲学校去，若人中仅有两名男生，求安排结果至少有一名男生的概率．
相关试题
，倾斜角为
的直线
过椭圆的左焦点
，与椭圆
交于
两点，若以
为直径的圆过椭圆的右焦点
，求
的值.
的两个焦点分别为
，离心率为
.
的方程；
分别为
，求线段
的中点
的轨迹方程，并说明轨迹是什么曲线.
底面
，其中
，
平面
锥
的体积
的余弦值（理科）
与曲线
相交于
两点，若
，求
的值.
，且经过点
，求椭圆的标准方程.
的双曲线的标准方程.推荐套卷
（本小题满分12分）下图为某校语言类专业N名毕业生的综合测评成绩（百分制）分布直方图，已知80-90分数段的学员数为21人
（1）求该专业毕业总人数N和90-95分数段内的人数；
（2）现欲将90-95分数段内的名人分配到几所学校，从中安排2人到甲学校去，若人中仅有两名男生，求安排结果至少有一名男生的概率．
粤公网安备 44130202000953号