已知关于x的一元二次方程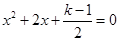
有两个不相等的实数根，k为正整数．
（1）求k的值；
（2）当次方程有一根为零时，直线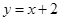
与关于x的二次函数
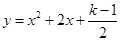的图象交于A、B两点，若M是线段AB上的一个动点，过点M作MN⊥x轴，交二次函数的图象于点N，求线段MN的最大值及此时点M的坐标；
（3）将（2）中的二次函数图象x轴下方的部分沿x轴翻折到x轴上方，图象的其余部分保持不变，翻折后的图象与原图象x轴上方的部分组成一个“W”形状的新图象，若直线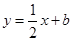
与该新图象恰好有三个公共点，求b的值．
相关试题
某水果批发商场经销一种高档水果，如果每千克盈利10元，每天可售出500千克，经市场调查发现，在进货价不变的情况下，若每千克涨价为1元，日销售量将减少20千克，现该商场要保证每天盈利6000元，同时又要使顾客得到实惠，那么每千克应涨价多少元？
已知二次函数y= -2x2+8x-6，完成下列各题：
（1）将函数关系式用配方法化为
的形式，并写出它的顶点坐标、对称轴．
（2）它的图像与x轴交于A,B两点，顶点为C,求S△ABC．
如图，某中学准备在校园里利用围墙的一段，再砌三面墙，围成一个矩形花园ABCD（围墙MN最长可利用22m），现在已备足可以砌50m长的墙的材料，试设计一种砌法，使矩形花园的面积为300m2．
相关知识点
推荐套卷
粤公网安备 44130202000953号