九(1)班组织班级联欢会,最后进入抽奖环节,每名同学都有一次抽奖机会.抽奖方案如下:将一副扑克牌中点数为“2”、“3”、“3”、“5”、“6”的五张牌背面朝上洗匀,先从中抽出1张牌,再从余下的4张牌中抽出1张牌,记录两张牌点数后放回,完成一次抽奖.记每次抽出两张牌点数之差为x,按下表要求确定奖项.
| 奖项 |
一等奖 |
二等奖 |
三等奖 |
 |
 |
 |
 |
(1)用列表或画树状图的方法求出甲同学获一等奖的概率;
(2)是否每次抽奖都会获奖,为什么?
相关知识点
推荐套卷
 的图象如图所示.
的图象如图所示.
 ,求二次函数的解析式;
,求二次函数的解析式;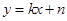 ,点
,点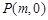 是x轴上的一个动点.若在(1)的条件下,过点P垂直于x轴的直线交这个一次函数的图象于点M,交二次函数
是x轴上的一个动点.若在(1)的条件下,过点P垂直于x轴的直线交这个一次函数的图象于点M,交二次函数 时,点M位于点N的上方,求这个一次函数的解析式;
时,点M位于点N的上方,求这个一次函数的解析式;  有实数根,请你构造恰当的函数,根据图象直接写出
有实数根,请你构造恰当的函数,根据图象直接写出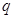 的最大值.
的最大值.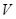 (单位:千米/时)是车流密度
(单位:千米/时)是车流密度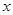 (单位:辆/千米)的函数,函数图象如图所示.
(单位:辆/千米)的函数,函数图象如图所示. 
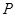 =车流速度
=车流速度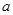 ,
,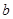 ,
, ,并且设置了相应的垃圾箱,“厨余垃圾”箱、“可回收物”箱和“其他垃圾”箱,分别记为A,B,C.
,并且设置了相应的垃圾箱,“厨余垃圾”箱、“可回收物”箱和“其他垃圾”箱,分别记为A,B,C.
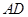 ∶
∶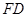 =1∶2,求⊙O的半径的长.
=1∶2,求⊙O的半径的长. 粤公网安备 44130202000953号
粤公网安备 44130202000953号