“十八大”报告一大亮点就是关注民生问题，交通问题已经成了全社会关注的热点.为了解新建道路的通行能力，某研究表明，某种情况下，车流速度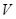
(单位：千米／时)是车流密度
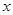(单位：辆／千米)的函数，函数图象如图所示. 
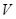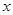（1）求关于的函数表达式；
（2）车流量是单位时间内通过观测点的车辆数，计算公式为：车流量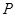
=车流速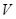度×车流密度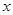.若车流速度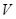低于80千米／时，求当车流密度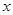为多少时，车流量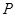(单位：辆／时)达到最大，并求出这一最大值．
相关试题
＋y2－3xy＝4．求下列各式的值：某初级中学为了解学生的身高状况，在1500名学生中抽取部分学生进行抽样统计，结果如下：
请你根据上面的图表，解答下列问题：
(1)此次抽样调查中样本容量为；
(2)m＝，n＝；
(3)补全频数分布直方图；
(4)请你估计该校1500名学生中身高处于160.5～170.5cm的人数约为人．
(1)求证：△ABC≌△CDE；
的解适
合x＋y＝2，求m的值．
相关知识点
推荐套卷
粤公网安备 44130202000953号