(本小题满分14分)已知抛物线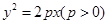 的焦 点为F,A是抛物线上横坐标为4、
的焦 点为F,A是抛物线上横坐标为4、
位于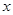 轴上方的点,A到抛物线准线的距离等于5.过A作AB垂直于
轴上方的点,A到抛物线准线的距离等于5.过A作AB垂直于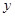 轴,垂足为B,OB的中点为M.
轴,垂足为B,OB的中点为M.
(1)求抛物线方程.
(2)以M为圆心,MB为半径作圆M,当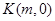 是
是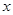 轴上一动点时,讨论直线AK与圆M的位置关系.
轴上一动点时,讨论直线AK与圆M的位置关系.
相关知识点
推荐套卷
(本小题满分14分)已知抛物线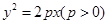 的焦 点为F,A是抛物线上横坐标为4、
的焦 点为F,A是抛物线上横坐标为4、
位于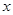 轴上方的点,A到抛物线准线的距离等于5.过A作AB垂直于
轴上方的点,A到抛物线准线的距离等于5.过A作AB垂直于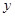 轴,垂足为B,OB的中点为M.
轴,垂足为B,OB的中点为M.
(1)求抛物线方程.
(2)以M为圆心,MB为半径作圆M,当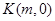 是
是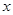 轴上一动点时,讨论直线AK与圆M的位置关系.
轴上一动点时,讨论直线AK与圆M的位置关系.