浑南“万达广场”五一期间举办“万达杯”游戏大赛.每5人组成一队,编号为1,2,3,4,5.在其中的投掷飞镖比赛中,要求随机抽取3名队员参加,每人投掷一次.假设飞镖每次都能投中靶面,且靶面上每点被投中的可能性相同.某人投中靶面内阴影区域记为“成功”(靶面为圆形, 为正方形).每队至少有2人“成功”则可获得奖品(其中任何两位队员“成功”与否互不影响).
为正方形).每队至少有2人“成功”则可获得奖品(其中任何两位队员“成功”与否互不影响).
(Ⅰ)某队中有3男2女,求事件A:“参加投掷飞镖比赛的3人中有男有女”的概率;
(Ⅱ)求某队可获得奖品的概率.
相关知识点
推荐套卷
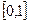 的函数
的函数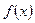 同时满足以下三个条件:
同时满足以下三个条件: ,总有
,总有 ;
; 且
且 ,则有
,则有 成立,并且称
成立,并且称 的值;
的值;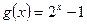 在区间
在区间 ,求证:
,求证: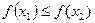
 与椭圆
与椭圆 交于
交于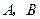 两点,记
两点,记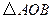 的面积为
的面积为 .
. ,
, 的条件下,
的条件下,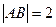 ,
,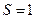 时,求直线
时,求直线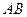 的方程.
的方程.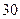 元,且每卖出一件产品,需向税务部门上交
元,且每卖出一件产品,需向税务部门上交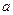 元(
元(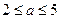 )的税收,设每件产品的日售价为
)的税收,设每件产品的日售价为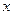 元(
元( ),根据市场调查,日销售量与
),根据市场调查,日销售量与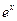 (
(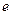 为自然对数的底数)成反比,已知每件产品的日售价为
为自然对数的底数)成反比,已知每件产品的日售价为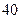 元,日销售量为
元,日销售量为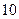 件。w.w.w..c.o.m
件。w.w.w..c.o.m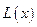 元与每件产品的日售价
元与每件产品的日售价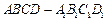 中,底面
中,底面 是直角梯形,
是直角梯形,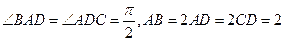
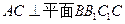
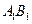 上是否存一点
上是否存一点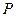 ,使得
,使得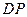 与平面
与平面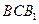 与平面
与平面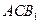 都平行?证明你的结论.
都平行?证明你的结论.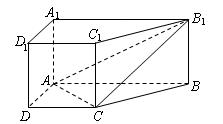
 (2)现从乙班这10名同学中随机抽取两
(2)现从乙班这10名同学中随机抽取两 名身高不低于
名身高不低于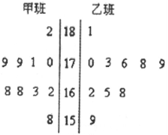
 粤公网安备 44130202000953号
粤公网安备 44130202000953号