⊙O为△ABC的外接圆，请仅用无刻度的直尺，根据下列条件分别在图1，图2中画出一条弦，使这条弦将△ABC分成面积相等的两部分（保留作图痕迹，不写作法）．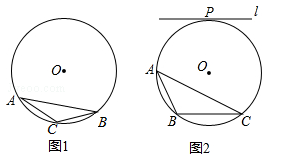
（1）如图1，AC=BC；
（2）如图2，直线l与⊙O相切于点P，且l∥BC．
；（2）sin30°+cos30°•tan60°．
（n为正整数）
时，试求 
的值”，其中
，请你判断该同学的答案是否正确，说出你的道理。
，再从“0，－2，2，4”中任选一个
值代入求原式的值.相关知识点
推荐套卷
⊙O为△ABC的外接圆，请仅用无刻度的直尺，根据下列条件分别在图1，图2中画出一条弦，使这条弦将△ABC分成面积相等的两部分（保留作图痕迹，不写作法）．
（1）如图1，AC=BC；
（2）如图2，直线l与⊙O相切于点P，且l∥BC．
粤公网安备 44130202000953号