一个棱柱的直观图和三视图（主视图和俯视图是边长为
的正方形，左视图是直角边长为的等腰三角形）如图所示，其中M、N分别是AB、AC的中点，G是DF上的一动点．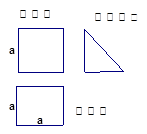
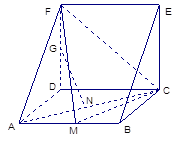
（Ⅰ）求证：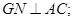
（Ⅱ）当FG=GD时，证明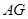
//平面FMC；
（Ⅲ）求三棱锥
的体积
相关试题
时取最大值2。
是集合
中的任意两个元素，
的最小值为
。
的值。
相关知识点
推荐套卷
一个棱柱的直观图和三视图（主视图和俯视图是边长为的正方形，左视图是直角边长为的等腰三角形）如图所示，其中M、N分别是AB、AC的中点，G是DF上的一动点．
（Ⅰ）求证：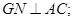
（Ⅱ）当FG=GD时，证明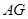//平面FMC；
（Ⅲ）求三棱锥的体积
粤公网安备 44130202000953号