操作:如图,在正方形ABCD中,P是CD上一动点(与C,D不重合),令三角板(一个锐角为30°)的直角顶点与点P重合,并且一条直角边始终过点B,另一直角边与正方形的某一边所在的直线交于点E.
探究:
(1)观察操作结果,哪一个三角形与△BPC相似?并说明理由.
(2)当点P位于CD的中点时,你找到的三角形与△BPC的相似比是多少?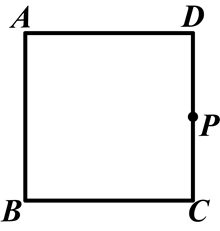
操作:如图,在正方形ABCD中,P是CD上一动点(与C,D不重合),令三角板(一个锐角为30°)的直角顶点与点P重合,并且一条直角边始终过点B,另一直角边与正方形的某一边所在的直线交于点E.
探究:
(1)观察操作结果,哪一个三角形与△BPC相似?并说明理由.
(2)当点P位于CD的中点时,你找到的三角形与△BPC的相似比是多少?