为了解学生参加社团的情况，从2010年起，某市教育部门每年都从全市所有学生中随机
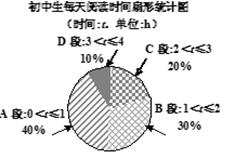
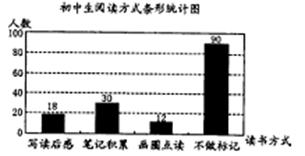
抽取2000名学生进行调查.图①、图②是部分调查数据的统计图（参加社团的学生每人只能报一项，根据统计图提供的信息解决下列问题：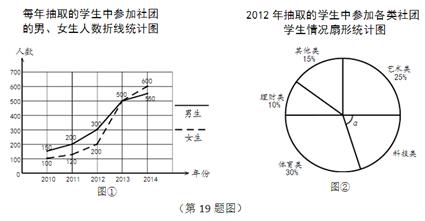
（1）求图②中“科技类”所在扇形的圆心角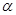
的度数；
（2）该市 2012 年抽取的学生中，参加体育类与理财类社团的学生共有多少人？
（3）该市 2014 年共有 50000 名学生，请你估计该市2014年参加社团的学生人数.
相关试题
如图，EF∥AD，∠1=∠2，∠BAC=70°。求∠AGD．请将解题过程填写完整。
因为EF∥AD，（已知）
所以∠2=_________．（）
又因为∠1=∠2，（已知）
所以∠1=∠3．（）
所以AB//________．（）
所以∠BAC+_______=180°．（）
又因为∠BAC=70°，（已知）
所以∠AGD=________．
相关知识点
推荐套卷
粤公网安备 44130202000953号