如果抛物线C1的顶点在抛物线C2上,同时,抛物线C2的顶点在抛物线C1上,那么,我们称抛物线C1与C2关联.
(1)已知两条抛物线①:y=x2+2x-1,②:y=-x2+2x+1,判断这两条抛物线是否关联,并说明理由;
(2)抛物线C1:y=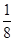 (x+1)2-2,动点P的坐标为(t,2),将抛物线C1绕点P(t,2)旋转180°得到抛物线C2,若抛物线C2与C1关联,求抛物线C2的解析式.
(x+1)2-2,动点P的坐标为(t,2),将抛物线C1绕点P(t,2)旋转180°得到抛物线C2,若抛物线C2与C1关联,求抛物线C2的解析式.
相关知识点
推荐套卷
如果抛物线C1的顶点在抛物线C2上,同时,抛物线C2的顶点在抛物线C1上,那么,我们称抛物线C1与C2关联.
(1)已知两条抛物线①:y=x2+2x-1,②:y=-x2+2x+1,判断这两条抛物线是否关联,并说明理由;
(2)抛物线C1:y=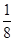 (x+1)2-2,动点P的坐标为(t,2),将抛物线C1绕点P(t,2)旋转180°得到抛物线C2,若抛物线C2与C1关联,求抛物线C2的解析式.
(x+1)2-2,动点P的坐标为(t,2),将抛物线C1绕点P(t,2)旋转180°得到抛物线C2,若抛物线C2与C1关联,求抛物线C2的解析式.