甲、乙两名运动员进行长跑训练,两人距终点的路程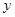 (米)与跑步时间
(米)与跑步时间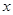 之间的函数关系如图所示,根据图象所提供的信息解答问题:
之间的函数关系如图所示,根据图象所提供的信息解答问题: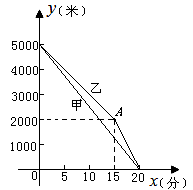
(1)他们在进行 米的长跑训练,在0<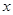 <15的时间内,速度较快的人是 (填“甲”或“乙”);
<15的时间内,速度较快的人是 (填“甲”或“乙”);
(2)求乙距终点的路程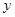 (米)与跑步时间
(米)与跑步时间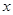 之间的函数关系式;
之间的函数关系式;
(3)当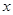 =15时,两人相距多少米?
=15时,两人相距多少米?
(4)在15<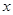 <20的时间段内,求两人速度之差.
<20的时间段内,求两人速度之差.
相关知识点
推荐套卷
甲、乙两名运动员进行长跑训练,两人距终点的路程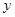 (米)与跑步时间
(米)与跑步时间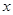 之间的函数关系如图所示,根据图象所提供的信息解答问题:
之间的函数关系如图所示,根据图象所提供的信息解答问题:
(1)他们在进行 米的长跑训练,在0<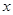 <15的时间内,速度较快的人是 (填“甲”或“乙”);
<15的时间内,速度较快的人是 (填“甲”或“乙”);
(2)求乙距终点的路程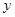 (米)与跑步时间
(米)与跑步时间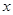 之间的函数关系式;
之间的函数关系式;
(3)当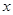 =15时,两人相距多少米?
=15时,两人相距多少米?
(4)在15<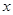 <20的时间段内,求两人速度之差.
<20的时间段内,求两人速度之差.