如图,跷跷板AB的一端B碰到地面时,AB与地面的夹角为18°,且OA=OB=3m.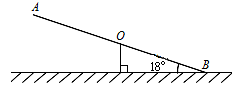
(1)求此时另一端A离地面的距离(结果精确到0.1);
(2)跷动AB,使端点A碰到地面,请画出点A运动的路线(保留画图痕迹),并求出点A运动路线的长.(结果保留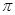 )(参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
)(参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
相关知识点
推荐套卷
如图,跷跷板AB的一端B碰到地面时,AB与地面的夹角为18°,且OA=OB=3m.
(1)求此时另一端A离地面的距离(结果精确到0.1);
(2)跷动AB,使端点A碰到地面,请画出点A运动的路线(保留画图痕迹),并求出点A运动路线的长.(结果保留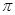 )(参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
)(参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)