(本小题满分12分)一种电子玩具按下按钮后,会出现红球或绿球.已知按钮第一次按下后,出现红球与绿球的概率都是 从按钮第二次按下起,若前次出现红球,则下一次出现红球、绿球的概率分别为
从按钮第二次按下起,若前次出现红球,则下一次出现红球、绿球的概率分别为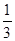 、
、 ;若前次出现绿球,则下一次出现红球,绿球的概率分别为
;若前次出现绿球,则下一次出现红球,绿球的概率分别为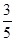 、
、
记第 次按下按钮后出现红的概率为Pn.
次按下按钮后出现红的概率为Pn.
(1)求P2的值;
(2)当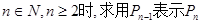 的表达式;
的表达式;
(3)求Pn关于n的表达式.
推荐套卷
(本小题满分12分)一种电子玩具按下按钮后,会出现红球或绿球.已知按钮第一次按下后,出现红球与绿球的概率都是 从按钮第二次按下起,若前次出现红球,则下一次出现红球、绿球的概率分别为
从按钮第二次按下起,若前次出现红球,则下一次出现红球、绿球的概率分别为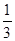 、
、 ;若前次出现绿球,则下一次出现红球,绿球的概率分别为
;若前次出现绿球,则下一次出现红球,绿球的概率分别为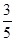 、
、
记第 次按下按钮后出现红的概率为Pn.
次按下按钮后出现红的概率为Pn.
(1)求P2的值;
(2)当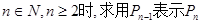 的表达式;
的表达式;
(3)求Pn关于n的表达式.