（本小题满分12分）某广场有一块不规则的绿地如图所示，城建部门欲在该地上建造一个底座为三角形的环境标志，小李、小王设计的底座形状分别为
，经测量
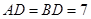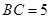米，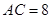
米，
米，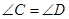
．
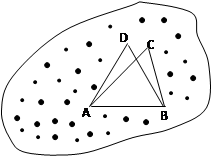
（Ⅰ）求
的长度；
（Ⅱ）若环境标志的底座每平方米造价为5000元，不考虑其他因素，小李、小王谁的设计使建造费用较低（请说明理由）？较低造价为多少？（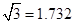
）
相关试题
（a、b、c是常数），且满足
上的单调性并证明
时，
求：
的前
项和为
，满足
，且
构成等比数列；
；
.推荐套卷
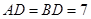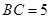（本小题满分12分）某广场有一块不规则的绿地如图所示，城建部门欲在该地上建造一个底座为三角形的环境标志，小李、小王设计的底座形状分别为，经测量米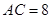，米，米，．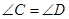
（Ⅰ）求的长度；
（Ⅱ）若环境标志的底座每平方米造价为5000元，不考虑其他因素，小李、小王谁的设计使建造费用较低（请说明理由）？较低造价为多少？（）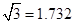
粤公网安备 44130202000953号