如图，点B、C、D都在⊙O上，过点C作AC∥BD交OB延长线于点A，连接CD，且∠CDB=∠OBD=30°，B=6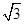
cm． 
（1）求证：AC是⊙O的切线；
（2）求由弦CD、BD与弧BC所围成的阴影部分的面积．（结果保留π）
；
；
；
；
相关知识点
推荐套卷
如图，点B、C、D都在⊙O上，过点C作AC∥BD交OB延长线于点A，连接CD，且∠CDB=∠OBD=30°，B=6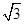cm．
（1）求证：AC是⊙O的切线；
（2）求由弦CD、BD与弧BC所围成的阴影部分的面积．（结果保留π）
粤公网安备 44130202000953号