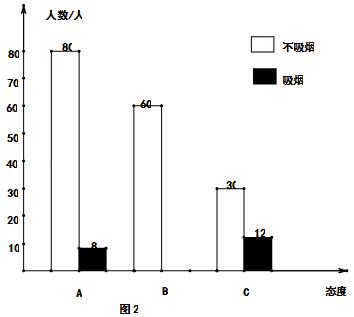
某校组织了一批学生随机对部分市民就是否吸烟以及吸烟和非吸烟人群对他人在公共场所吸烟的态度(分三类:A表示主动制止;B表示反感但不制止,C表示无所谓)进行了问卷调查,根据调查结果分别绘制了如下两个统计图。请根据图中提供的信息解答下列问题:
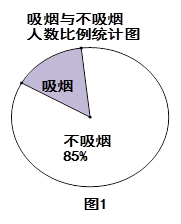
(1)图1中,"吸烟"类人数所占扇形的圆心角的度数是多少?
(2)这次被调查的市民有多少人?
(3)补全条形统计图
(4)若该市共有市民760万人,求该市大约有多少人吸烟?
相关知识点
推荐套卷
某校组织了一批学生随机对部分市民就是否吸烟以及吸烟和非吸烟人群对他人在公共场所吸烟的态度(分三类:A表示主动制止;B表示反感但不制止,C表示无所谓)进行了问卷调查,根据调查结果分别绘制了如下两个统计图。请根据图中提供的信息解答下列问题:


(1)图1中,"吸烟"类人数所占扇形的圆心角的度数是多少?
(2)这次被调查的市民有多少人?
(3)补全条形统计图
(4)若该市共有市民760万人,求该市大约有多少人吸烟?